Floyd's loop detection (and correction)
October 03, 2019
This article is about the algorithm by R. W. Floyd for detecting and removing a loop in a linked list data structure. It is a classical question during IT job interview, generating a lot of badly written web pages on the topic.
The problem
Suppose to have a linked list data structure where each block has a pointer to the next one. The invariant is that the last element must point to NULL. Now suppose that, for some reason, this invariant is violated and this results in a loop. The image below represents the faulty linked list (boxes and arrows in black). We want an efficient way to identify the last node \(Y\) and restore its pointer to NULL.
Trivial solutions include memorizing the memory location of visited blocks.
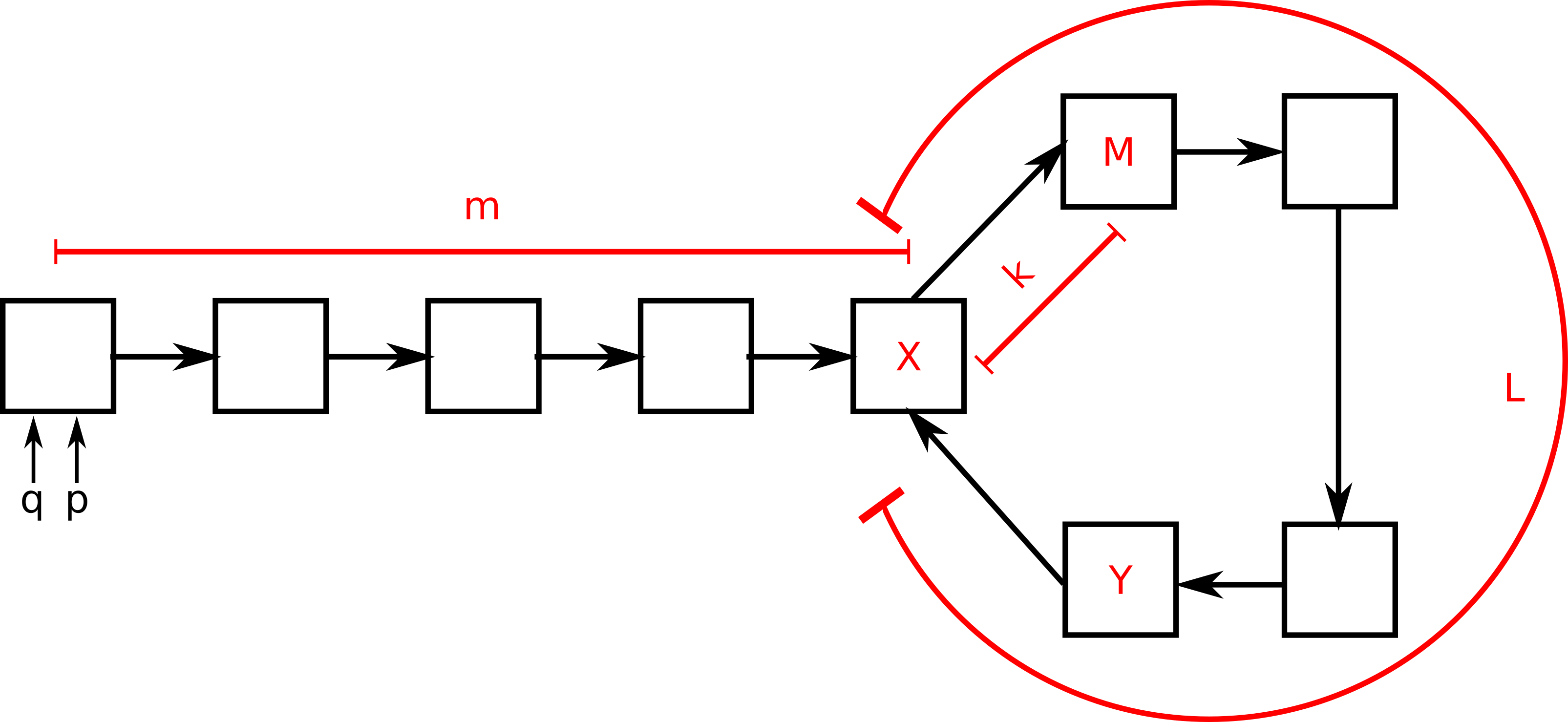
Floyd’s way
Floyd’s algorithm can be used to detect and correct a loop like this in linear time and using a constant amount of memory. What is interesting it is not the algorithm itself but the mathematical reasoning behind it.
The algorithm works in two phases:
- Identify node \(M\);
- initialize two pointers \(p,q\) to the list head;
- move \(p\) one block ahead, \(q\) two blocks ahead until end is reached or \(q==p\).
- Identify node \(Y\);
- initialize two pointers, \(q\) to the list head and \(p\) to \(M\);
- until \(q==p\), set \(Y=p\) and move \(p,q\) one block ahead.
Why it works
We need to show the effectiveness of the algorithms for the two phases separately. But first a bit of notation:
| Symbol | Meaning | Value in example |
|---|---|---|
| \(X\) | block of loop beginning | |
| \(m\) | distance between list head and \(X\) | 4 |
| \(k\) | distance between \(X\) and \(M\) | 1 |
| \(L\) | loop length | 5 |
Let’s start considering phase 1; if there is no loop then eventually \(q\) reaches the end before \(p\) (because it is going double its speed). If there is a loop then eventually \(p,q\) are gonna be inside it. Inside the loop, let \(d_k=q-p (\mod L)\) be the distance between the two pointers at step \(k\). Then, \(d_{k+1}=q+2-p-1(\mod L) = q-p+1 (\mod L) = d_k+1 (\mod L)\)
Eventually, hence \(d_{\bar{k}} = L (\mod L) = 0\) and, therefore, \(p==q\) and we reach \(M\) (note we need just existence not uniqueness).
Phase 2 is about proving that moving \(p,q\) one block at the time they meet in \(X\).
During phase 1, we moved \(q\) for \(m+k+\bar{q}L\) blocks and \(p\) for \(m+k+\bar{p}L\) blocks, where \(\bar{q},\bar{p}\) indicate the amount of complete loops for \(q,p\) respectively. Since they finally met in \(M\) and \(p\) was moving twice the speed of \(q\) we can say that
\[m+k+\bar{p}L=2m+2k+2\bar{q}L\] \[\implies m = (2\bar{q}-\bar{p})L - k\]At the beginning of phase 2 \(q\) is initialized to the list head and \(p\) to \(M\) and we move them one block ahed at the time. When \(q\) reaches \(X\) it has moved exactly \(m\) blocks, which means that \(p\) has moved \((2\bar{q}-\bar{p})L - k\) blocks, and, since it started from distance \(k\) from \(X\) it has arrived exactly where the loop begins, at \(X\).